Acronychal Rising. [from ἀκρόνυχος 'beginning of night']. The last visible rising of a celestial object on the eastern horizon after sunset. On the next night, the object will not be visible when it rises because the Sun will have moved further east and sky will not be dark enough. On the previous day the object was more easily visible as it rose because the Sun was further west. In ancient times, the acronychal rising of a star or group of stars was sometimes used to determine the seasons. Hesiod, around 700 BCE for example, notes the acronychal rising of Arcturus —which happened around 24th February— in Works and Days (564–70) as a suitable time for the pruning of vines.
Almagest. The conventional English title for Ptolemy's great manual of astronomy completed and published around 150 CE. The name is a borrowing from the Arabic al-majisṭī which is itself a borrowing from the shortened Greek title Μεγίστη 'Greatest' which in turn is a colloquial derivation from the fuller form Ἡ Μεγάλη Σύνταξις 'The Great Treatise'. However, the original title was Μαθηματικὴ Σύνταξις 'Mathematical Treatise'. Sometimes the book is known by its later Latin title Syntaxis. Along with Euclid's Elements of Geometry it is one of the two great scientific books that have come down to us from antiquity in their entirety.
In it, Ptolemy gives a complete mathematical description of the sky as understood at the time, drawing on the works of several previous astronomers, chiefly Hipparchos. The work consists of 13 chapters (ancient books) arranged as follows:
- Mathematical preliminaries.
- Principles and practice of observation.
- The Sun.
- The Moon 1.
- The Moon 2.
- Eclipses.
- The stars 1.
- The stars 2.
- The planets 1 (Mercury).
- The planets 2 (Venus and Mars).
- The planets 3 (Jupiter and Saturn).
- The planets 4 (retrogradations and stations).
- The planets 5 (elongations and latitudes).
The Almagest presents a development of the standard geocentric model of the sky at the time which in various forms had been widely, though not universally, accepted for around five centuries. A spherical stationary Earth was situated at the centre of the Universe. Around it there revolved in order of increasing distance: the Moon, Mercury, Venus, the Sun, Mars, Jupiter, Saturn, and the stars. Apart from the stars, which were arranged on a sphere centred on the Earth, all the other celestial objects revolved in little circles called epicycles (invented by Apollonios of Perga in the C3rd BCE) whose centres revolved around the Earth on larger circles called deferents. The deferents were not centred on the Earth itself but on a point in space somewhat displaced from it called the eccentre. The celestial bodies rotated on their epicycles at a uniform rate and the centres of the epicycles rotate at a uniform rate too, but not around the eccentre, since Ptolemy devised a second point in space, the equant, around which all the celestial bodies could be seen as to rotate at a uniform rate. All these mathematical constructions were made in order to accommodate the apparent irregularities, such as retrogradations, in the motions of the celestial bodies.
The two books on the stars contain tables of 1022 stars arranged in 48 constellations (one more than recognised by Hipparchos). Although he implies that all the observations were made by himself using an epoch of 138 CE, suspicion has been cast over the last two centuries that many of the positions recorded by Ptolemy were really those of Hipparchos systematically altered to take account of precession.
Because it so large (around 150,000 words) and comprehensive, the Almagest rendered most other general books on astronomy (apart from some specialised and introductory ones) redundant with the result that many were no longer copied and are now lost. It became the standard work on astronomy throughout later antiquity and the middle ages. It was translated into Arabic in the C9th CE and into Latin (from the Arabic) by Gerard of Cremona in 1175 CE. It was only superceded by the work of Copernicus, Tycho and Kepler in the late C16th CE. Up to the limit of observational precision available to naked eye astronomy at the time, the system of the Almagest accounted pretty thoroughly, but not always accurately, for the phenomena it described. Theoretically, it was appealing because the idea of of uniform circular motion had been a long standing preference, ever since Plato, for the motions of the heavens. However, the devices of the eccentre and in particular the equant, that Ptolemy had been forced to invent by the observational data, were often disliked. Indeed, Copernicus' motivation for his heliocentric system (which consequently required more epicycles) was largely the desire to get rid of the hated equant.
Standard text: Heiberg, J. L. (1898, 1903). Syntaxis Mathematica. Claudii Ptolemaei, opera quae exstant omnia, vols. 1.1 and 1.2, Teubner ed. Leipzig.
English translation: Toomer, G. J. (1984, 1998). Ptolemy's Almagest, 2nd edition. London 1998.
Altitude (a). The vertical angular distance, measured in degrees, of a celestial object above or below the horizon. Along with azimuth it is one of the two coordinates of the horizontal coordinate system. It ranges from –90° to +90°.
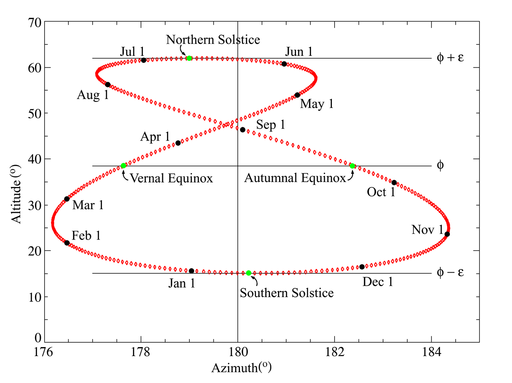 |
| Image: Wikimedia Commons |
The image shows a plot of the position of the sun at 12:00 noon at the Royal Observatory, Greenwich (latitude 51.4791° north, longitude 0°) during 2006. The horizontal axis is the azimuth angle in degrees (180° is facing south). The vertical axis is the altitude in degrees above the horizon. The first day of each month is shown in black, and the solstices and equinoxes are shown in green. It can be seen that the equinoxes occur at an altitude of ϕ = 90° – 51.4791° = 38.5209°, and the solstices occur at ϕ ± ε where ε is the axial tilt of the Earth, 23.439°. Analemmas are often found inscribed on sundials so that the conversion from apparent solar time to mean solar time can be performed immediately.
Anomalistic Month.
Anomalistic Year.
 |
A reconstuction of the Antikythera Mechanism in the
National Archaeological Museum, Athens.
Photo by the author 2011.
|
In the last few decades extensive scientific work has been carried out on the badly corroded mechanism and much of its mode of operation has been deduced by patient analysis and reconstruction, although some of the details remain uncertain or disputed. The date of construction is thought to be variously c. 205 BCE (Carman 2017), c. 150–100 BCE (Freeth et al. 2006, 2008) or c. 80 BCE (Price 1974). If, as is likely, it was built in Rhodes (a centre for philosophy and science at the time), it may have been designed either by Hipparchos or a student of his (middle date), or Posidonios (later date). The latter is supported by the report of Cicero ( De Natura Deorum 2.88, 33–34) who knew Posidonios and visited Rhodes in 89 BCE, reporting that the latter had constructed a device resembling an orrery. Nowadays however, most scholars agree that it was made in the C2nd BCE, thus ruling out Posidonios.
 |
Fragment A containing the large 14cm gearwheel and the remains
of four gear trains behind it. Image: Wikimeida Commons.
|
Many of the main astronomical cycles known in antiquity are represented in the mechanism, including: the Metonic Cycle of 19 years = 235 months = 6940 days, and the Kallippic Cycle of 76 years = 940 months = 27759 days, both of which approximate recurring Moon phases; and the Saros Cycle of 223 months = 6585.3211 days, and the Exeligmos Cycle of 669 synodic months = 19755.9633 days, which may be used to predict eclipses.
Of significance is the discovery that while the fundamental mechanism is best suited for the latitude of Rhodes, the month names belong to the Corinthian family, specifically those of Epiros. It seems, therefore, that the device was one of many manufactured in Rhodes but modified for a client living in Epiros, probably the city of Ambrakia or Dodona.
Carman, Christián C. (2017).'The Final Date of the Antikythera Mechanism'. Journal for the History of Astronomy. Vol. 48(3) 312–32.
Freeth T. et al. (2006). 'Decoding the Antikythera Mechanism: Investigation of an Ancient Astronomical Calculator.' Nature, Volume 444, Issue 7119, 587-91.
Freeth T. et al. (2008). 'Calendars with Olympiad display and eclipse prediction on the Antikythera Mechanism'. Nature, Volume 454, 31st July, 614-17.
Iversen, Paul A. (2017). 'The Calendar on the Antikythera Mechanism and the Corinthian Family of Calendars'. Hesperia: The Journal of the American School of Classical Studies at Athens, 86.1 (January–March), 129–203. Price, D. de S. (1974). 'Gears from the Greeks: The Antikythera Mechanism — A Calendar Computer from ca. 80 BC.' Transactions of the American Philosophical Society, New Series, 64.7.
Voulgaris, Aristeidis et al. (2018).'Conclusions from the Functional Reconstruction of the Antikythera Mechanism'. Journal for the History of Astronomy. Vol. 49(2) 216–38.
Apocatastasis.
Apsis.
Archaic Era. A conventional period of Greek history which runs from the emergence of city-states and alphabetic writing around 800 BCE to the end of the Persian Wars in 479 BCE. It followed the Greek dark ages (c. 1100 – c. 800 BCE) and was followed by the Classical Era (479 – 323 BCE).
Arcturus.
Armilliary Sphere.
Asterism. A group of stars that are either very conspicuous or make a familiar pattern. Examples are the Pleiades in the constellation of Taurus or the Plough (Big Dipper) in Ursa Major.
Astrology.
Astronomical Year Numbering. A system of year numbering introduced by the astronomer Jacques Cassini (Tables Astronomiques) in 1740, although the idea goes back to Kepler's Rudolphine Tables. It follows the normal BCE/CE (BC/AD) numbering system but allows for a year 0, so as to facilitate easy computation of intervals. Thus, we have the equivalences:
–2 instead of 3 BCESo that, the difference in years between, for example, –150 (151 BCE) and +250 (250 CE) is 400, obtained simply by adding the absolute values. In the proleptic Julian Calendar, year 0 (and also –4, –8, etc.) is a leap year.
–1 instead of 2 BCE
0 instead of 1 BCE
1 instead of 1 CE
2 instead of 2 CE
etc.
Athenian Calendar. There was actually more than one Athenian calendar, but the principal one, more properly known as the Athenian Festival Calendar, is the one that mainly regulated the lives of citizens and the one which bears comparison with the calendars of other Greek city–states. Like all ancient Greek calendars it was lunisolar and consisted of 12 or 13 months of 29 or 30 days each, with the beginning of the month determined by the new moon. And like the calendars of other city-states it only had relevance in the city and district of its origin since its principal motivation was to provide the correct dates for the observance of religious festivals. Unlike other Greek city-states, however, the Athenian year began in summer with the first new moon after the summer solstice. The list of months (one of the few that is known in full) is as follows:
| Season | Month | Julian Equivalent |
|---|---|---|
| Summer (Θέρος) | 1. Hekatombaion (Ἑκατομβαιών) | July/August |
| 2. Metageitnion (Μεταγειτνιών) | August/September | |
| 3. Boedromion (Βοηδρομιών) | September/October | |
| Autumn (Φθινόπωρον) | 4. Pyanepsion (Πυανεψιών) | October/November |
| 5. Maimakterion (Μαιμακτηριών) | November/December | |
| 6. Poseideon (Ποσειδεών) | December/January | |
| Winter (Χεῖμα) | 7. Gamelion (Γαμηλιών) | January/February |
| 8. Anthesterion (Ἀνθεστηριών) | February/March | |
| 9. Elaphebolion (Ἑλαφηβολιών) | March/April | |
| Spring (Ἔαρ) | 10. Mounuchion (Μουνυχιών) | April/May |
| 11. Thargelion (Θαργηλιών) | May/June | |
| 12. Skirophorion (Σκιροφοριών) | June/July |
Each month was on average 29.5 days long, and the standard cycle of 12 months amounted to 354 or 355 days, 10 or 11 days short of the year. In order to keep the calendar synchronised with the seasons, one of the months was repeated from time to time (on average every three years), usually Poseideon, but sometimes Hekatombaion, Metageitnion, Gamelion or Anthesterion. In the Classical Era this was not done according to any system but by official decree whenever it seemed appropriate. In this case the year was 384 days long.
The names of the months were derived either from religious festivals or from activities or gods associated with festivals. In some cases the festivals were obscure and no longer took place during the C5th BCE, reflecting the antiquity of the calendar, whilst relatively new major festivals such as the City Dionysia or Panathenaia are not directly reflected in the names. Some month names are shared with the calendars of Ionia, although the times of the year do not generally coincide. Since Ionia was colonised by the Athenians during the C11th BCE, this shows how old some aspects of the calendar were. Like many people today, it is likely that the average C5th BCE Athenian did not know much about the origins of the calendar they used.
The months were either 29 or 30 days long but the lengths were not fixed. A particular month was declared to be 'hollow' (29 days) or 'full' (30 days) just a couple of days before its end when the day of the next new Moon could be estimated. Very occasionally, extra days were added by the Archon (chief magistrate) in the middle of a month in order to accommodate some pressing administrative purpose, such as extra time required to prepare for the City Dionysia in 271 BCE (SEG 14.65). When such a discrepancy arose the date would be referred to as κατ' ἄρχοντα 'according to the Archon' as opposed to κατὰ θεόν 'according to the god'.
We do not know how the day of the new Moon was determined but it is unlikely to have been by direct observation, which is difficult to do. Probably it was just estimated by watching the waning Moon over a few days. We have some tangential evidence to show that the whole business was not very accurate. In Aristophanes' play The Clouds (607–626) the chorus reports a conversation with the Moon where she complains that people have not been following her movements correctly and getting their days mixed up. As a result of all this it is rarely possible to be exact as to the day of the year when something occurred in ancient Athens (or Greece generally) when using only contemporary calendrical evidence.
The last day of the old month was called ἕνη καὶ νέα 'old and new' and the first day of the new month was called νουμηνία 'new Moon'. The rest of the month had numbered days according to a three fold division of the Moon's phase: waxing (αὐξομένη), full (πλήθουσα), waning (φθίνουσα):
| Waxing | Full | Waning |
|---|---|---|
| New Moon | 11th | Later 10th |
| Waxing 2nd | 12th | Waning 9th |
| Waxing 3rd | 13th | Waning 8th |
| Waxing 4th | 14th | Waning 7th |
| Waxing 5th | 15th | Waning 6th |
| Waxing 6th | 16th | Waning 5th |
| Waxing 7th | 17th | Waning 4th |
| Waxing 8th | 18th | Waning 3rd |
| Waxing 9th | 19th | Waning 2nd |
| Waxing 10th | Earlier 10th | Old and New |
The two consecutive '10ths' on days 21 and 22 and the switch to reverse counting probably had something to do with anticipation of the next new Moon. When the month was to have 29 days, the waning 2nd day was eliminated. The system seems to have evolved for convenience and flexibility rather than accuracy.
Alongside the festival calendar another calendar was also in use, the so called Prytanic Calendar, which may be regarded as the civic or political calendar. Each of the ten tribes of Athens were granted one prytany (presidential month) during which they held the presidency, responsible for steering business through the executive council of the state. When the system was first devised in the early C5th BCE, it seems that the prytanies alternated between 36 and 37 days to give a total of 365 days, thus paying no attention to the Moon or the festival calendar. However, after 407 BCE, it was synchronised with the festival calendar as shown below.
Months 1 to 4: 36 days (39 days in leap years)
Months 5 to 10: 35 days (38 in leap years)
giving a total of 354 or 384 days. The prytanic months were not named, just numbered, and the days within them were also simply numbered in sequence.
In addition to these state–sanctioned calendars a third calendar was also in use. We may term this the sidereal calendar. It was the traditional calendar used all over Greece by farming communities and relied upon the risings, settings and culminations of stars, much as Hesiod (fl. 700 BCE) had indicated in his poem Works and Days. Because this was astronomically determined and not subject to cultural or political interference, it was an objective measure of the course of the year. It was used not only by farmers, and not only by astronomers, but also by anyone wanting to record events that could be compared all over Greece. Thus, it was sometimes used by Thucydides to date events in his History of the Peloponnesian War. In describing the siege of Plataea, for example, a wall is described as being finished and a garrison stationed (2.78.2) 'about the time of the heliacal rising of Arcturus' (περὶ ἀρκτούρου ἐπιτολάς) which in 429 BCE happened in the last week of September.
Hannah, Robert (2005). Greek and Roman Calendars. London.
Parke, H. W. (1977). Festivals of the Athenians. London.
Pritchett, William Kendrick (2001). Athenian Calendars and Ekklesias. Amsterdam.
Atmospheric refraction. The phenomenon whereby light is bent (refracted) as it travels though air of varying density. It causes the apparent position of distant objects to deviate from their true positions. Typically, objects near the horizon, where the air is denser, appear to higher than they really are and even objects below the horizon to appear to be above it. It is responsible for desert mirages and the apparent flattening of the Sun's disk at sunrise and sunset.
The amount of refraction is a function of the humidity, pressure and temperature of the air though which the light passes as well as the thickness of the air. Since these are varying quantities, it is very difficult to predict exactly the amount of refaction that may occur at any one time. Generally, however, the higher up a a celestial object is in the sky, the less it will be subject to refraction and the more accurately its position can be determined.
Two simple empirical formulae for refraction R (in minutes of arc) are given below:
R = cot [ ha + 7.31 / ( ha + 4.4 ) ] (Bennett 1982)where ha is the apparent altitude and ht is the true altitude in degrees. The formulae should be accurate for steady atmospheric conditions where the pressure is 101 kPa and the temperature is 10°C. If the pressure P and the Temperature T are known, the value of R can be multiplied by a factor of [P/101][283/(273+T)] to achieve greater accuracy. A graph of the first formula is shown below.
R = 1.02 cot [ ht + 10.3 / ( ht + 5.11 ) ] (Sæmundsson 1986)

It can be seen that the amount of refraction becomes quite severe below about 5° above the horizon rising to typically 35 minutes of arc at the horizon. This is more than the Sun's apparent diameter which means that when the Sun appears to be just fully above the horizon it is actually completely below it.
It seems likely that Greek astronomers of the Hellenistic and Roman periods were aware of atmospheric refraction in the sense that objects near the horizon were sometimes observed to be not quite in the right position or difficult to locate precisely, but there was no understanding of its cause or any attempt to quantify it. The only known reference to the effect occurs in Ptolemy's Almagest (9.2; H2.210).
Bennett, G.G. (1982). 'The Calculation of Astronomical Refraction in Marine Navigation'. Journal of Navigation. 35 (2): 255–259.Azimuth (A). In astronomy, azimuth is the horizontal angular distance in degrees between a celestial object and the direction of north as measured in an easterly direction. Along with altitude it is one of the two coordinates of the horizontal coordinate system. It ranges from 0° to 360°.
Sæmundsson, Þorsteinn (1986). 'Astronomical Refraction'. Sky and Telescope. 72: 70
